Materials science relies heavily on the concepts of stress and strain. Stress refers to the forces applied to a material, while strain describes the resulting deformation. Though related, these two terms have distinct meanings and applications. This article will explain the stress and strain definition and key differences between stress and strain and why they matter for materials engineering.
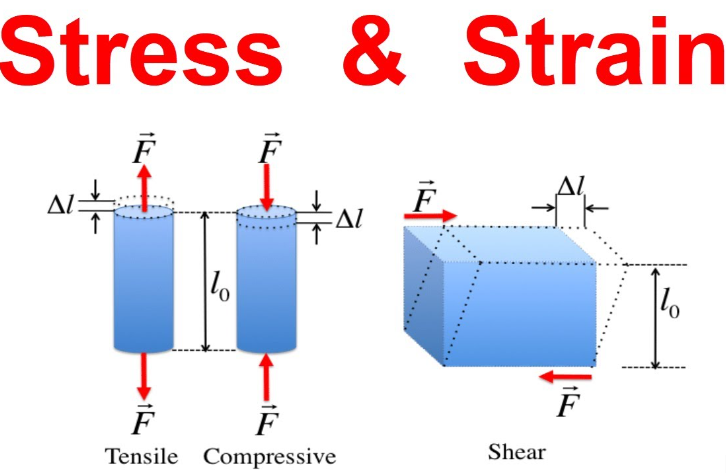
Stress and Strain Definition
Stress is the internal resisting force per unit area that develops inside a material when an external load is applied, measured in Pascals, while strain is the resulting fractional change in shape or size—such as elongation, compression, or shear—expressed as a dimensionless ratio of deformation to original dimension.
What is Stress?
Stress is defined as the force per unit area acting on a material. It is caused by external forces that pull, push, twist or shear the material. The common types of stresses are tensile, compressive, shear, and torsional stress. Stress is calculated by dividing the applied force (F) by the cross-sectional area (A) it acts on:
- Stress = F/A
Stress causes materials to deform. At low levels, the deformation is elastic and reversible. But high stresses can cause permanent plastic deformation or even fracture. Understanding a material’s stress response is crucial for proper design and material selection.
What is Strain?
Strain describes the deformation that occurs in a material under stress. It measures the change in shape and dimensions produced by applied forces. Strain is calculated as the change in length (∆L) divided by the original length (L0):
- Strain = ∆L/L0
Strains can be tensile, compressive, or shear, matching the type of applied stress. The strain response depends on the material and stress level. At low stresses, strain is elastic, and the material returns to its original shape when stress is removed. At higher stresses, permanent plastic strain occurs.
Stress vs Strain
Understanding the nuanced difference between stress and strain is foundational in materials science and structural engineering. Analyzing both reveals insights into material behavior that inform critical design decisions. Their relationship also allows the calculation of key mechanical properties. Mastering stress and strain principles is crucial for engineers across many fields.
| Property | Stress | Strain |
| Definition | Force per unit area applied to a material | Deformation or change in dimensions caused by stress |
| Symbol | σ | ε |
| Units | Pascals (Pa), psi | Dimensionless or % |
| Type | Tensile, compressive, shear, torsional | Tensile, compressive, shear, volumetric |
| Cause | External forces | Deformation due to applied stress |
| Effect | Deforms material, changes properties | Elastic deformation or permanent plastic deformation |
| Behavior | Reversible (elastic) or permanent (plastic) | Recoverable (elastic) or permanent (plastic) |
| Failure | Fracture if stress exceeds strength | Fracture if strain exceeds ductility |
| Calculation | Stress = Force / Area | Strain = (Change in length) / (Original length) |
| Measurement | Load cells, strain gauges | Extensometers, strain gauges |
| Related Properties | Young’s modulus, shear modulus | Poisson’s ratio, ductility |
What is the Difference Between Stress and Strain
Stress
- Definition: Stress is the internal force per unit area within a material that arises due to externally applied forces.
- Formula:
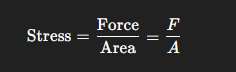
- Unit: Pascals (Pa) or N/m²
- Type: Measures the intensity of internal forces acting within a body.
- Analogy: Think of stress like the pressure a material feels when being pushed or pulled.
Strain
- Definition: Strain is the measure of deformation of a material due to stress. It is the relative change in shape or size.
- Formula:

- Unit: It is dimensionless (a ratio)
- Type: Measures how much a material stretches or compresses.
- Analogy: If stress is the force applied, strain is how much the object stretches because of it.
What is Tensile Strain?
Tensile strain is a measure of how much a material stretches or elongates when subjected to a pulling (tensile) force. It is defined as the ratio of the increase in length to the material’s original length. Mathematically, tensile strain = (change in length) ÷ (original length), and since it’s a ratio of two lengths, it has no units. Tensile strain helps engineers understand how ductile or elastic a material is—materials with higher tensile strain before breaking are generally more stretchable. It’s a key factor in assessing structural integrity under tension.
Strain Definition Engineering
In engineering, strain is defined as the measure of deformation representing the displacement between particles in a material body relative to a reference length. It quantifies how much a material stretches, compresses, or distorts when subjected to an external force. Mathematically, strain is the ratio of the change in dimension (such as length) to the original dimension, expressed as:
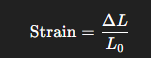
Strain is dimensionless (no units) and can be tensile (stretching), compressive (shortening), or shear (angular distortion), depending on the type of load applied. It’s a critical concept in material science and structural engineering for evaluating how materials respond to stress.
Examples of Stress and Strain of Different Materials
- Metals:
– Ductile metals like aluminum and copper yield and deform plastically under tensile stress. Their stress-strain curves show elastic deformation followed by plastic flow.
– Brittle metals like cast iron fracture with minimal plastic deformation. Their stress-strain curves are linear until sudden fracture.
– Steel displays an elastic region, yield point, strain hardening, and ultimate tensile strength before fracture.
- Polymers:
– Rigid polymers like PMMA experience linear elastic deformation followed by brittle fracture.
– Ductile polymers like polyethylene undergoes elastic deformation, yielding, necking, and drawing before failure.
– Elastomers like rubber display extreme elastic deformation with minimal plastic flow. Their stress-strain curves are nonlinear.
- Ceramics:
– Most ceramics are brittle, showing elastic deformation and sudden fracture with no plastic flow. Their stress-strain curves are linear.
– Some ceramics are semi-brittle, exhibiting some non-linear behavior and microcracking.
- Composites:
– Fiber-reinforced composites typically display linear elastic behavior followed by fiber breakage and plastic matrix deformation.
– Response depends on fiber type (glass, carbon) and matrix material (polymer, metal, ceramic).
- Concrete:
– Concrete shows an initial elastic region, followed by microcracking and plastic deformation before fracture. Stress-strain curves are nonlinear.
- Wood:
– Wood exhibits an initial elastic region, yield point, and plastic deformation with ductile splintering failure parallel to grain direction.
Difference Between Tensile Stress and Tensile Strain
| Property | Tensile Stress | Tensile Strain |
|---|---|---|
| Definition | Force applied per unit cross-sectional area | Extension per unit original length |
| Formula | σ=FA\sigma = \frac{F}{A}σ=AF | ϵ=ΔLL0\epsilon = \frac{\Delta L}{L_0}ϵ=L0ΔL |
| Units | Pascals (Pa or N/m²) | Dimensionless (no units) |
| Effect | Causes material to stretch or elongate | Measures how much the material has stretched |
| Type | Mechanical resistance (cause) | Deformation response (effect) |
Difference Between Axial Stress and Axial Strain
| Property | Axial Stress | Axial Strain |
|---|---|---|
| Definition | Stress along the axis of a structural member | Deformation (change in length) along the same axis |
| Direction | Acts perpendicular to the cross-section | Measures axial elongation or compression |
| Units | Pascals (Pa or N/m²) | Dimensionless |
| Use | Helps determine internal force resistance | Helps predict elongation or shortening of structures |
Stress vs Strain Units
| Property | Stress | Strain |
|---|---|---|
| Units | Pascals (Pa), N/m² | No units (it’s a ratio) |
| Type | Measures internal force intensity | Measures relative deformation |
Stress vs Strain Relationship
The relationship is typically linear in the elastic region and described by Hooke’s Law:
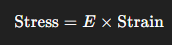
- E is Young’s Modulus (a material constant).
- In this region, a material deforms proportionally to the applied force.
- Once stress exceeds the elastic limit, the relationship becomes nonlinear, leading to permanent deformation or failure.
Stress vs Strain in Psychology
In psychology, stress and strain are used metaphorically to describe mental and emotional pressure:
| Term | Psychological Stress | Psychological Strain |
|---|---|---|
| Meaning | The mental pressure or demand placed on a person | The emotional or physical response to that stress |
| Cause/Effect | Stress is the external trigger (e.g. workload, trauma) | Strain is the internal reaction (e.g. anxiety, burnout) |
| Analogy | Stress = external force | Strain = internal effect or damage |

