Materials deform in different ways depending on how you load them. Push equally from all sides and the volume shrinks; slide the top face while the bottom is fixed and the shape skews. Engineers quantify these behaviors with elastic moduli that tie stress to strain within the linear elastic range. Two of the most widely used are the bulk modulus, which captures resistance to uniform compression, and the shear modulus, which captures resistance to shape change under tangential forces.
These modulus values help predict how substances will deform under different types of loads, making them fundamental in designing structures, machines, and countless real-life applications. Here, we are going to take a close look at both bulk and shear modulus, their definitions, formulas, units, calculation methods, and how they differ and relate to other elastic moduli like Young’s modulus.
1. What is Shear Modulus (Definition)
Shear modulus, also known as the modulus of rigidity, measures a material’s ability to resist shear stress. It tells us how much a material will deform when a shear force is applied. The shear modulus describes an object’s tendency to shear, or change shape at constant volume, when acted upon by opposing forces. It is defined as the ratio of shear stress to shear strain. When a force is applied parallel to one face of an object while the opposite face is held fixed by another equal force, the material deforms, this deformation is described by the shear modulus.
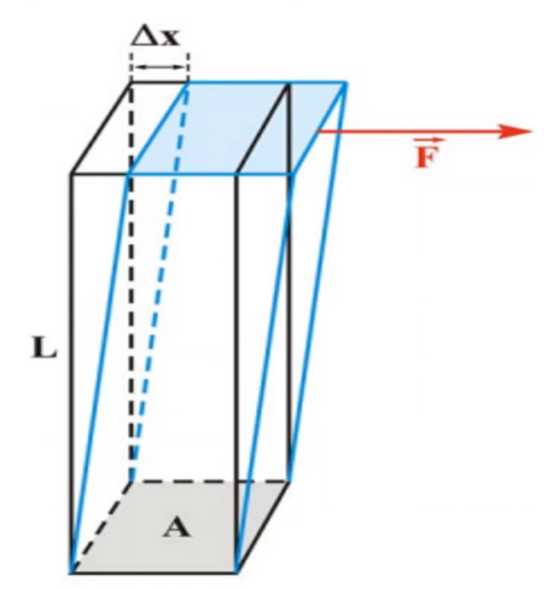
If you imagine pushing the top of a deck of cards while holding the bottom steady, that sliding motion is similar to shear stress. The shear modulus is sometimes called the modulus of rigidity because the higher its value, the more rigid the material is—meaning it is less likely to bend or change shape under shear forces.
Shear Modulus Symbol
The shear modulus is commonly represented by the symbol G (sometimes also μ or S). In equations and technical literature, you will often see it as G.
Shear Modulus Units
Shear modulus is defined as the ratio of shear stress (force per unit area) to shear strain (a dimensionless quantity), so its units are the same as those for pressure. In the International System of Units (SI), the shear modulus is measured in pascals (Pa), where 1 pascal equals 1 newton per square meter (N/m²). For large values, gigapascals (GPa) are often used, with 1 GPa being 1 billion pascals. In the United States customary system, shear modulus may be expressed in pounds per square inch (psi) or kips per square inch (ksi).
Shear Modulus Equation (Formula) & How To Calculate
The formula for shear modulus is:
G = τ / γ
where
- G = Shear modulus
- τ = Shear stress (force applied per unit area, F/A)
- γ = Shear strain (the resulting angular deformation)
Alternatively, the formula can be written in terms of measurable quantities:
G = (F x L) / (A x Δx)
Here,
- F = Applied force (parallel to one face)
- L = Original length over which the deformation occurs
- A = Area of the face parallel to the applied force
- Δx = Displacement (distance the top moves relative to the bottom)
For small angles, the shear strain γ can be approximated as γ ≈ tanϕ ≈ ϕ, where ϕ is the angle of deformation in radians.
Shear Modulus Equation with Poisson’s Ratio
When Young’s modulus (EEE) and Poisson’s ratio (ν\nuν) are known, the shear modulus can also be calculated using:
G = E / 2(1+ν)
This relationship is important in engineering because it allows you to determine the shear modulus from other commonly measured material properties.
How To Find Shear Modulus
To find the shear modulus, you need to determine the shear stress and the shear strain.
- Calculate Shear Stress (τ\tauτ):
Shear stress is the force applied parallel to the surface divided by the area over which the force is applied:τ = F / A - Calculate Shear Strain (γ\gammaγ):
Shear strain is the relative displacement (Δx\Delta xΔx) divided by the original length (LLL):γ = Δx / L - Calculate Shear Modulus (G):
Substitute these values into the main formula:G = τ/γ
Example Calculation
For a cube with side length LLL subjected to a shear force FFF, if the top face moves by a distance Δx\Delta xΔx:
G = (F × L) / (A × Δx)
If you are given Young’s modulus and Poisson’s ratio, use the alternative formula above.
How To Measure Shear Modulus (Experimental Methods)
The shear modulus is typically measured using mechanical tests that apply a known shear force and measure the resulting deformation. The most common methods include:
- Torsion Test:
A cylindrical rod or hollow cylinder of the material is twisted using a torque. The angular displacement and applied torque are recorded, and the shear modulus is determined as the slope of the stress-strain curve. - Torsion Pendulum Test:
This test uses a rod with a disc attached, twisted and allowed to oscillate. The period of oscillation is measured, and the shear modulus is calculated based on the oscillation frequency. - Direct Shear Test:
Special fixtures apply pure shear to notched specimens, allowing direct measurement of shear strain and stress. - Optical Methods (e.g., Moiré Interferometry):
Fine patterns on the specimen’s surface deform under load, creating interference patterns that can be analyzed to determine displacement fields and calculate shear strain.
Dynamic mechanical analysis is used for viscoelastic materials, applying oscillating shear stress at various frequencies to measure both elastic and viscous components of the shear modulus.
Shear Modulus of Different Materials
The shear modulus varies greatly among different materials, reflecting each material’s ability to resist deformation under shear forces. Below is a table listing the typical shear modulus values for a wide range of common materials in gigapascals (GPa), pounds per square inch (PSI), and kilo-pounds per square inch (KSI). (Note: 1 GPa = 145,038 PSI = 145 KSI)
| Material | Shear Modulus (GPa) | Shear Modulus (PSI) | Shear Modulus (KSI) |
|---|---|---|---|
| Steel (mild) | 79.0 | 11,460,000,000 | 11,460 |
| Stainless Steel | 77.0 | 11,170,000,000 | 11,170 |
| Aluminum | 25.5 | 3,700,000,000 | 3,700 |
| Brass | 39.0 | 5,660,000,000 | 5,660 |
| Copper | 44.0 | 6,380,000,000 | 6,380 |
| Titanium | 41.0 | 5,950,000,000 | 5,950 |
| Tungsten | 161.0 | 23,340,000,000 | 23,340 |
| Magnesium | 17.0 | 2,470,000,000 | 2,470 |
| Nickel | 76.0 | 11,020,000,000 | 11,020 |
| Lead | 5.6 | 812,000,000 | 812 |
| Zinc | 43.0 | 6,240,000,000 | 6,240 |
| Carbon Fiber (uni) | 30–50 | 4,350,000,000–7,250,000,000 | 4,350–7,250 |
| Concrete | 10–21 | 1,450,000,000–3,050,000,000 | 1,450–3,050 |
| Glass (Soda-lime) | 29.0 | 4,210,000,000 | 4,210 |
| Epoxy Resin | 1.2–3.5 | 174,000,000–508,000,000 | 174–508 |
| Selenium | 3.6 | 522,000,000 | 522 |
| Polycarbonate | 2.4 | 348,000,000 | 348 |
| Polyethylene (HDPE) | 0.82 | 119,000,000 | 119 |
| Rubber (natural) | 0.0004–0.001 | 58–145,000 | 0.058–0.145 |
| Wood (parallel grain) | 0.8–1.4 | 116,000,000–203,000,000 | 116–203 |
| Ice | 2.3 | 334,000,000 | 334 |
| Diamond | 478.0 | 69,300,000,000 | 69,300 |
2. What is Bulk Modulus (Definition)
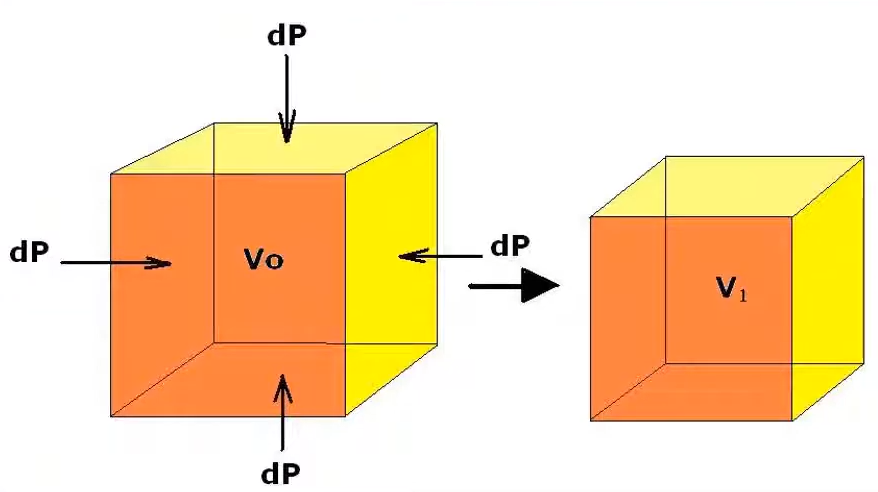
The bulk modulus of a substance is a measure of how resistant that substance is to compressibility. It defines the material’s resistance to uniform compression. Bulk modulus describes how difficult it is to decrease the volume of a material when external pressure is applied equally from all directions. When a compressive force acts uniformly on all surfaces of an object, the object undergoes a decrease in volume, and the bulk modulus quantifies this resistance. For example, if a solid or fluid is compressed from all sides, the resulting reduction in its volume is related to the applied pressure through this property.
Bulk Modulus Symbol
Bulk modulus is commonly represented by the capital letter K or sometimes B. Both symbols are used interchangeably in literature and engineering practice.
Bulk Modulus Units
Bulk modulus is defined as the ratio of pressure change to the resulting fractional decrease in volume. In the International System of Units (SI), the bulk modulus is measured in pascals (Pa), specifically newtons per square meter (N/m²). Because bulk modulus values are typically large, gigapascals (GPa) are often used (1 GPa = 1,000,000,000 Pa). In some contexts, bulk modulus can also be given in pounds per square inch (psi).
Bulk Modulus Equation – Bulk Modulus Formula & How To Calculate
The mathematical formula for bulk modulus is:
K = Volumic Stress / Volumic Starin = – V × (dP/dV)
Or, for finite changes:
K = – (ΔP) / (ΔV / V₀)
Where:
- K = Bulk modulus
- ΔP = Change in pressure applied to the object
- ΔV = Change in volume due to the pressure
- V₀ = Original volume
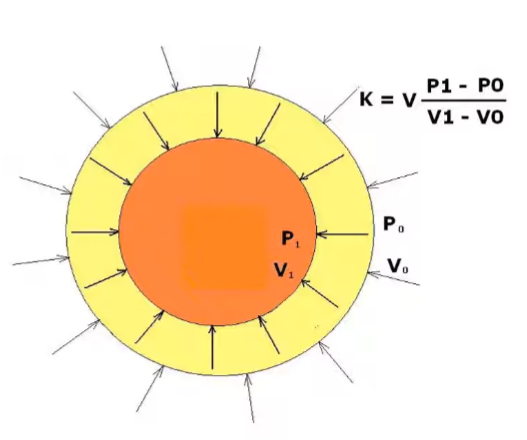
The negative sign appears because an increase in pressure leads to a decrease in volume. Thus, bulk modulus is always taken as a positive value.
How To Find Bulk Modulus
To determine the bulk modulus, you need to know the change in pressure applied to a material and the corresponding change in volume. The relative (fractional) change in volume is divided into the applied pressure difference. For example, if you submerge a sphere in water, the pressure from the water compresses the sphere, causing a small decrease in its volume.
The procedure involves:
- Measuring the initial volume of the object (V₀)
- Applying a known increase in pressure (ΔP)
- Measuring the resulting change in volume (ΔV)
- Substituting these values into the formula:
K = – (ΔP) / (ΔV / V₀)
How To Measure Bulk Modulus
Bulk modulus can be measured experimentally by enclosing a sample in a chamber and applying pressure from all directions. The change in the sample’s volume is then measured. For example, when a steel or aluminum sphere is submerged to great depths in the ocean, the increased pressure causes a measurable, though small, reduction in its volume. The relationship between this compression and the pressure applied yields the bulk modulus.
For fluids, pressure is often applied with a piston or hydraulic system, and the volume change is observed. For solids, the pressure can be applied using a pressure vessel, and precise instruments measure the resulting volume contraction. The negative sign in the formula is consistent with the fact that an increase in pressure decreases the volume.
Bulk Modulus Equation with Poisson’s Ratio
Bulk modulus can also be related to Young’s modulus (E) and Poisson’s ratio (ν) using the following equation:
K = E / 3(1−2ν)
Here,
- K = Bulk modulus
- E = Young’s modulus
- ν = Poisson’s ratio
This relationship is useful when direct measurements of bulk modulus are unavailable, but other elastic constants are known.
Bulk Modulus of Different Materials
Bulk modulus varies widely among different materials, which reflects their compressibility. Here are typical values for several common materials:
| Material | Bulk Modulus (GPa) | Bulk Modulus (psi) | Bulk Modulus (ksi) |
|---|---|---|---|
| Steel | 160 | 23,200,000,000 | 23,200,000 |
| Stainless Steel | 160 | 23,200,000,000 | 23,200,000 |
| Aluminum | 70 | 10,150,000,000 | 10,150,000 |
| Brass | 100 | 14,500,000,000 | 14,500,000 |
| Copper | 140 | 20,300,000,000 | 20,300,000 |
| Titanium | 110 | 15,950,000,000 | 15,950,000 |
| Tungsten | 310 | 45,000,000,000 | 45,000,000 |
| Magnesium | 45 | 6,530,000,000 | 6,530,000 |
| Nickel | 180 | 26,100,000,000 | 26,100,000 |
| Lead | 46 | 6,670,000,000 | 6,670,000 |
| Zinc | 70 | 10,150,000,000 | 10,150,000 |
| Carbon Fiber | 30–50 | 4,350,000,000–7,250,000,000 | 4,350,000–7,250,000 |
| Concrete | 14–30 | 2,030,000,000–4,350,000,000 | 2,030,000–4,350,000 |
| Glass | 35–55 | 5,080,000,000–7,980,000,000 | 5,080,000–7,980,000 |
| Selenium | 14 | 2,030,000,000 | 2,030,000 |
| Rubber | 2–4 | 290,000,000–580,000,000 | 290,000–580,000 |
| Water | 2.2 | 319,000,000 | 319,000 |
| Air | 0.0001 | 14.5 | 0.0145 |
| Diamond | 442 | 64,100,000,000 | 64,100,000 |
3. Shear Modulus vs Bulk Modulus: What are the Differences Between Them?
The main distinction between these moduli lies in the type of deformation they describe. Bulk modulus measures resistance to uniform compression. It quantifies how much a material’s volume decreases under equal pressure from all sides. For instance, when a solid sphere is submerged in a fluid, the inward forces compress it and reduce its volume; this process is governed by bulk modulus.
Shear modulus, on the other hand, is concerned with deformation where the volume of the material remains constant, but its shape changes. When forces are applied tangentially to parallel surfaces (like pushing the top of a block while the bottom stays fixed), layers within the material slide past each other. The bulk modulus relates to compressibility, while the shear modulus relates to rigidity and resistance to sliding or shape change.
Bulk modulus is primarily used for fluids and gases, which are subject to volumetric compression, but also to solids under hydrostatic pressure. Shear modulus is more relevant to solids that resist shape change when subject to tangential forces.
As we have introduced each modulus above with details, here we use the table below to sum up the differences between bulk modulus and the shear modulus:
| Aspect | Bulk Modulus | Shear Modulus |
|---|---|---|
| Symbol | K (or B) | G |
| What It Measures | Resistance to uniform compression (change in volume) | Resistance to shape change (shear deformation) |
| Type of Stress | Volumetric (hydrostatic) stress | Shear (tangential) stress |
| Type of Strain | Volumetric strain (ΔV/V₀) | Shear strain (γ, angular distortion) |
| Formula | K=−ΔP/(ΔV/V₀) | G=τ/γ |
| Physical Scenario | Compression from all directions (e.g., submerging in fluid) | Sliding or deformation under parallel forces |
| Units | Pascal (Pa), GPa, N/m² | Pascal (Pa), GPa, N/m² |
| Typical Materials | Solids, liquids, gases (bulk compression) | Mainly solids (shear deformation) |
| Volume Change | Yes (decreases under pressure) | No (volume remains almost constant) |
| Shape Change | No (shape remains) | Yes (shape changes, volume stays nearly constant) |
| Related to | Compressibility | Rigidity |
| Relation to Other Moduli | K=E/3(1−2ν) | G=E2/(1+ν) |
Bulk Modulus vs Shear Modulus Example
To better understand the differences between bulk modulus and shear modulus in practice, let’s consider two scenarios: one involving volumetric compression (bulk modulus) and another involving shape deformation (shear modulus).
Example 1: Bulk Modulus in Action
Suppose an aluminum ball with a radius of 0.5 meters is dropped to the bottom of the sea, where the pressure is 150 atmospheres. The bulk modulus of aluminum is given as 70×109 pascals. When submerged, the inward pressure exerted by the fluid acts on all surfaces of the sphere, compressing it from every direction and causing its volume to decrease.
Using the bulk modulus formula:
ΔV = − ΔP⋅V₀ / K
First, convert the pressure to pascals:
ΔP=150×101325=15,198,750 Pa
The original volume of the sphere:
V0=4/3 x π x r3= 4/3 x π x (0.5)3= 0.5236 m3
Now substitute into the formula:
ΔV = − (15,198,750×0.5236) / 70 × 109
ΔV ≈ −1.137×10−4m3
The negative sign indicates a decrease in volume. This small reduction demonstrates how the bulk modulus governs the compressibility of materials under uniform pressure.
Example 2: Shear Modulus in Action
Now, consider a cube of aluminum with side length 10 centimeters (0.1 meters). A horizontal shear force of 50,000 newtons is applied to the top of the cube, causing it to deform slightly, while the bottom remains fixed. The shear modulus for aluminum is 25× 109 pascals.
The displacement (Δx) of the top surface can be found with:
Δx = (F x L) / (G x A)
where:
- F=50,000
- L=0.1 m (height of the cube)
- A=0.01 m2(top surface area)
- G=25× 109 Pa
Plugging in the values:
Δx = (50,000×0.1) / (25×109×0.01)
Δx = 5,000 / (2.5×108)
Δx = 2×10−5 m
This extremely small displacement illustrates how the shear modulus measures a material’s resistance to shape change under parallel forces.
4. Shear Modulus and Bulk Modulus Relation
Shear modulus and bulk modulus are both part of the family of elastic moduli, constants that describe how a material responds to stress and strain. Along with Young’s modulus (E) and Poisson’s ratio (ν\nuν), these values are interrelated for isotropic, linear elastic materials.
The mathematical relationships connecting them are:
G = E / 2(1+ν)
K = E / 3(1−2ν)
This means that if two of the moduli and Poisson’s ratio are known, the others can be calculated. These equations are particularly important in materials science and engineering design, where not every modulus is measured directly.
5. Shear Modulus and Bulk Modulus Conversion
For practical applications, the ability to convert between shear modulus and bulk modulu is very useful. These conversions rely on the equations above. For example:
K = 2G(1+ν) / 3(1−2ν)
G = 3K(1−2ν) / 2(1+ν)
Here, ν\nuν is Poisson’s ratio, which relates lateral and longitudinal strain in a material under tension or compression. These equations allow engineers to calculate one modulus when the other and Poisson’s ratio are known, providing flexibility in material selection and analysis.
6. Young’s Modulus vs Shear Modulus vs Bulk Modulus (Difference & Relation)
Young’s modulus, shear modulus, and bulk modulus are all specific cases of the general concept of modulus of elasticity, which describes the relationship between stress and strain in the linear, elastic region of a material’s behavior.
- Young’s modulus (E): Measures resistance to change in length (tensile or compressive strain) under axial force.
- Bulk modulus (K): Measures resistance to change in volume under uniform pressure from all directions.
- Shear modulus (G): Measures resistance to shape change under tangential forces.
The stress-strain curve for a metal bar under tension is used to define Young’s modulus. For compression from all sides, the same proportional relationship exists between stress and strain, but it is described by bulk modulus. When shape changes occur without a change in volume, as in shearing, the proportional relationship is described by shear modulus.
Each of these moduli provides a unique insight into how a material will behave under different types of forces or loading conditions.
7. FAQs about Shear Modulus vs Bulk Modulus
Q: What is bulk modulus in fluid Mechanics?
A: Bulk modulus in fluid mechanics refers to a measure of how resistant a fluid is to compression when subjected to an increase in pressure from all directions. It quantifies how difficult it is to decrease the volume of a fluid when it is uniformly compressed.
Q: What are typical units for these moduli?
A: Both bulk modulus and shear modulus are measured in pascals (Pa) or gigapascals (GPa). In some regions, pounds per square inch (psi) is used.
Q: When is bulk modulus most important?
A: Bulk modulus is especially useful for understanding the compressibility of fluids and the response of solids under hydrostatic pressure.
Q: How are these moduli measured?
A: Bulk modulus is measured by applying uniform pressure and observing the resulting change in volume. Shear modulus is often measured using torsion tests, where a rod or cylinder is twisted and the resulting deformation is recorded.
Q: Why is the negative sign used in the bulk modulus formula?
A: The negative sign is included because an increase in pressure causes a decrease in volume, making the strain negative.
Q: Can you convert between shear and bulk modulus?
A: Yes, using Poisson’s ratio and Young’s modulus, you can convert between these moduli using established equations.

