Have you ever written a quick line of code to check if a number is even (x % 2 == 0) and called it the “modulus” operator? Or perhaps you’ve seen a negative number become positive and wondered about the math behind it? You’re interacting with two different sides of the same linguistic coin. Join us as we’ll find out the difference between modulo vs modulus.

What’s Modulus?
Modulus meaning is a measure of a material’s stiffness or resistance to deformation when a force is applied. It quantifies how much a material will stretch, compress, or change shape under stress. The most common type is Young’s modulus, which measures tensile or compressive stiffness along a length. Materials with a high modulus are stiff and deform very little under load, while materials with a low modulus are more flexible. Other forms include shear modulus (resistance to twisting or shearing) and bulk modulus (resistance to uniform compression). In essence, modulus helps engineers and scientists predict how materials will behave under various forces, ensuring they can design structures and products safely and efficiently.
What’s the Application of the Modulus?
The modulus function (or absolute value function) is used to determine the non-negative value of a number, regardless of its sign. For example, consider the function f(x)=∣x∣f(x) = |x|f(x)=∣x∣. If x=−3x = -3x=−3, then f(−3)=−(−3)=3f(-3) = -(-3) = 3f(−3)=−(−3)=3 because xxx is less than 0. If x=3x = 3x=3, then f(3)=3f(3) = 3f(3)=3 since xxx is greater than 0. When x=0x = 0x=0, f(0)=0f(0) = 0f(0)=0. This demonstrates that the modulus function always outputs a non-negative value, and importantly, f(−3)=f(3)f(-3) = f(3)f(−3)=f(3), meaning ∣−3∣=∣3∣=3|-3| = |3| = 3∣−3∣=∣3∣=3. This property is widely applied in mathematics and real-world problems where only the magnitude matters, such as distance calculations, error measurements, and financial modeling.
Properties of Modulus Function
The modulus function, denoted as ∣x∣|x|∣x∣, has several important properties that are useful in solving equations and inequalities:
1. Non-Negativity:
The modulus function always produces a non-negative output for any real number xxx.
- If ∣x∣=a|x| = a∣x∣=a and a>0a > 0a>0, then x=±ax = \pm ax=±a.
- If ∣x∣=0|x| = 0∣x∣=0, then x=0x = 0x=0.
- If ∣x∣=a|x| = a∣x∣=a and a<0a < 0a<0, there is no solution, because the modulus can never be negative.
2. Absolute Value Inequalities:
- For a>0a > 0a>0:
- ∣f(x)∣<a|f(x)| < a∣f(x)∣<a ⇒ −a<f(x)<a-a < f(x) < a−a<f(x)<a
- ∣f(x)∣>a|f(x)| > a∣f(x)∣>a ⇒ f(x)<−af(x) < -af(x)<−a or f(x)>af(x) > af(x)>a
- For a<0a < 0a<0:
- ∣f(x)∣<a|f(x)| < a∣f(x)∣<a ⇒ no solution
- ∣f(x)∣>a|f(x)| > a∣f(x)∣>a ⇒ valid for all real values of f(x)f(x)f(x)
3. Algebraic Properties:
- ∣−x∣=∣x∣|-x| = |x|∣−x∣=∣x∣
- ∣x−y∣=0|x – y| = 0∣x−y∣=0 ⇔ x=yx = yx=y
- ∣x+y∣≤∣x∣+∣y∣|x + y| \le |x| + |y|∣x+y∣≤∣x∣+∣y∣ (Triangle inequality)
- ∣x−y∣≥∣∣x∣−∣y∣∣|x – y| \ge ||x| – |y||∣x−y∣≥∣∣x∣−∣y∣∣
- ∣xy∣=∣x∣⋅∣y∣|xy| = |x| \cdot |y|∣xy∣=∣x∣⋅∣y∣
- ∣x/y∣=∣x∣/∣y∣|x / y| = |x| / |y|∣x/y∣=∣x∣/∣y∣, for y≠0y \neq 0y=0
Note: Property 2 is particularly useful for solving absolute value inequalities, allowing you to convert them into standard inequalities that are easier to handle.
What’s Modulo?
Modulo meaning (often written as “mod”) is a mathematical operation that finds the remainder when one number is divided by another. For example, in the expression 17mod 517 \mod 517mod5, 17 divided by 5 equals 3 with a remainder of 2, so 17mod 5=217 \mod 5 = 217mod5=2. Modulo is widely used in programming, cryptography, and number theory because it helps determine cyclical patterns, wraparound values, and divisibility. Essentially, while division gives you a quotient, the modulo operation tells you what’s left over after dividing.
What’s the Application of the Modulo?
The modulo operation has many practical applications across mathematics, computer science, and everyday problem-solving. In programming, it’s commonly used to determine whether a number is even or odd, cycle through array indices, or implement wrap-around behavior in circular buffers. In cryptography, modulo arithmetic underpins many encryption algorithms, such as RSA, where calculations are performed within a finite number system. It’s also used in calendar calculations (finding the day of the week for a given date), in hash functions to distribute data evenly across storage, and in gaming for repeating patterns or rotations. Essentially, modulo helps manage remainders, cycles, and periodic behavior efficiently.
Properties of Modulo Function
The modulo function computes the remainder when one integer is divided by another. Its key properties include:
- Range of Output:
- For a mod na \bmod namodn, the result is always in the range 0≤a mod n<n0 \le a \bmod n < n0≤amodn<n when n>0n > 0n>0.
- Equivalence Relation:
- If two numbers differ by a multiple of nnn, they are equivalent modulo nnn:
a≡b (mod n)a \equiv b \ (\text{mod } n)a≡b (mod n) ⇔ nnn divides (a−b)(a – b)(a−b).
- If two numbers differ by a multiple of nnn, they are equivalent modulo nnn:
- Addition Property:
- (a+b) mod n=((a mod n)+(b mod n)) mod n(a + b) \bmod n = ((a \bmod n) + (b \bmod n)) \bmod n(a+b)modn=((amodn)+(bmodn))modn
- Subtraction Property:
- (a−b) mod n=((a mod n)−(b mod n)+n) mod n(a – b) \bmod n = ((a \bmod n) – (b \bmod n) + n) \bmod n(a−b)modn=((amodn)−(bmodn)+n)modn
- Multiplication Property:
- (a⋅b) mod n=((a mod n)⋅(b mod n)) mod n(a \cdot b) \bmod n = ((a \bmod n) \cdot (b \bmod n)) \bmod n(a⋅b)modn=((amodn)⋅(bmodn))modn
- Exponentiation Property:
- (ak) mod n=((a mod n)k) mod n(a^k) \bmod n = ((a \bmod n)^k) \bmod n(ak)modn=((amodn)k)modn
- Division Property (with inverse):
- Division in modulo arithmetic is only possible if the divisor has a modular inverse under the modulus nnn.
Modulus vs Modulo, What’s the Difference?
Although “modulus” and “modulo” sound similar, they refer to different concepts in mathematics:
- Modulus (|x|):
- Refers to the absolute value of a number.
- It measures the distance from zero, ignoring the sign.
- Example: ∣3∣=3|3| = 3∣3∣=3 and ∣−3∣=3|-3| = 3∣−3∣=3.
- Applications: Distance calculations, physics problems, error magnitudes.
- Modulo (a mod n):
- Refers to the remainder after division of one number by another.
- Example: 17mod 5=217 \mod 5 = 217mod5=2 because 17 divided by 5 leaves a remainder of 2.
- Applications: Programming (array wrapping, cyclic counters), cryptography, hashing, calendar calculations.
| Feature / Aspect | Modulus (|x|) | Modulo (a mod n) |
|---|---|---|
| Definition | Absolute value of a number | Remainder after division of one number by another |
| Operation | Removes the sign of a number | Divides and finds the remainder |
| Output | Always non-negative | Between 0 and n-1 (for positive modulus n) |
| Mathematical Symbol | |x| | a mod n |
| Example | |3| = 3, |-3| = 3 | 17 mod 5 = 2, 22 mod 7 = 1 |
| Applications | Distance, physics, error magnitudes | Programming, cyclic arrays, cryptography, hashing |
| Type of Arithmetic | Real numbers / magnitude | Integer / modular arithmetic |
| Sign of Result | Never negative | Depends on implementation; often non-negative |
| Focus | Magnitude / size | Remainder / division cycles |
Modulus vs Modulo Operator
- Modulus (Mathematical Concept)
Definition: The modulus is the remainder after division of one number by another. Formally: For integers 𝑎 a and 𝑛 > 0 n>0, the modulus is the remainder 𝑟 r when 𝑎 a is divided by 𝑛 n. Mathematically,
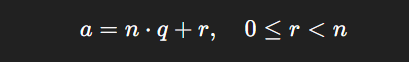
where 𝑞 q is the quotient, and 𝑟 r is the modulus. Example: 17 m o d 5 = 2 17mod5=2 (because 17 = 5 ⋅ 3 + 2 17=5⋅3+2)
Note: Modulus is a concept in number theory and mathematics in general. It’s about “what remains after division
2. Modulo Operator (Programming/Computer Science)
- Definition: The modulo operator (often written as
%in languages like Python, C, Java, etc.) calculates the remainder after integer division. - Behavior: Most programming languages follow slightly different rules when dealing with negative numbers:
- Python:
-17 % 5 = 3(always returns a non-negative remainder) - C/C++:
-17 % 5 = -2(remainder can be negative)
- Python:
Key takeaway: The modulo operator implements the modulus concept in code, but the behavior with negatives may differ depending on the programming language.
Modular Arithmetic vs Modulo
Modulo (Operation)
- Definition: The modulo operation finds the remainder after division of one number by another.
- Symbol: Usually written as
a mod nora % n. - Purpose: It’s a single calculation—“what is left over when aaa is divided by nnn?”
- Example:
17mod 5=217 \mod 5 = 217mod5=2
(17 divided by 5 leaves a remainder of 2.)
- Use case: Often used in programming, cryptography, hashing, and determining periodic behaviors.
Modular Arithmetic
- Definition: Modular arithmetic is a system of arithmetic for integers where numbers “wrap around” after reaching a certain value, called the modulus.
- Concept: Instead of just one calculation, it’s an entire arithmetic system where operations like addition, subtraction, and multiplication are performed modulo nnn.
- Example: With modulus 5:
3+4≡2 (mod 5)3 + 4 \equiv 2 \ (\text{mod } 5)3+4≡2 (mod 5)
(Because 3+4=73 + 4 = 73+4=7 and 7mod 5=27 \mod 5 = 27mod5=2) 4⋅3≡2 (mod 5)4 \cdot 3 \equiv 2 \ (\text{mod } 5)4⋅3≡2 (mod 5)
(Because 4⋅3=124 \cdot 3 = 124⋅3=12 and 12mod 5=212 \mod 5 = 212mod5=2)
- Use case: Modular arithmetic is fundamental in number theory, cryptography (RSA, Diffie-Hellman), computer science (hashing, cyclic buffers), and clock arithmetic.
What Is Modulus Math?
Modulus math deals with remainders — what’s left over after one number is divided by another. The modulus operator is written as “mod” or “%” in programming.
Example Calculations
| Expression | Explanation | Result |
|---|---|---|
| 7 mod 3 | 7 ÷ 3 = 2 remainder 1 | 1 |
| 10 mod 4 | 10 ÷ 4 = 2 remainder 2 | 2 |
| 15 mod 5 | 15 ÷ 5 = 3 remainder 0 | 0 |
| 23 mod 6 | 23 ÷ 6 = 3 remainder 5 | 5 |

